I love John Mason and although I’ve even quoted it myself a few times, I think I don’t wholeheartedly agree with the statement “it is the ways of thinking that are rich, not the task itself”. Let’s face it: some math problems are better than others, and choosing the right one for students to explore is a crucial step in shaping their mathematical learning journey.
Here’s the first blog post featuring what I hope will be a series of problems that have a lot of potential for students to engage with the type of thinking that encapsulates the essence of what it means to work mathematically:
The goal here is to have students find the fraction of each region one-by-one, easiest to hardest, largest to smallest. The first square is easy enough to get started, but hard enough to feel the need to work it out for yourself. The second square is less obvious for students, but rewards some patient problem solving as students realise the square is a third of the preceding rectangle. The third square leans heavily on the premise that students will correctly assume that the first square is one-quarter, the next is a quarter of that, and so on. As students work through each square, they might even get some extra fractions practice.
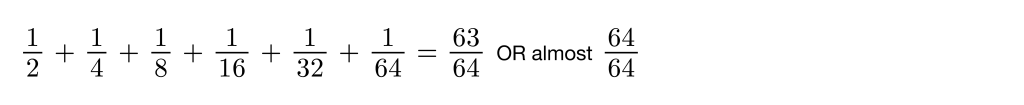
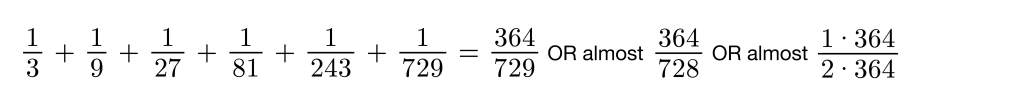

My hope here is that students have already cottoned on to a pattern between the first fraction in each sum and the shaded fraction that is being approached in each square. My hope is that they might not need this next prompt, but in case they do, here it is:
There’s a lot that this problem does, but it’s more what it doesn’t do, which I love so much:
- It’s not open ended. If a math problem could be an infinity pool, this would be it. The end of the problem is not obvious until you’re at it, but reaching it doesn’t disappoint.
- It’s not written as “Find the sum of the infinite series to determine the shaded proportion of each unit square to determine the general case for infinite series that approach 1/n blah blah blah.” I’m thankful for that and I bet my students are too.
- It’s not presented using any actual fraction notation. Students can bring in the mathematical reasoning when they are ready, and it’s ok for it to lag a little behind their intuition.
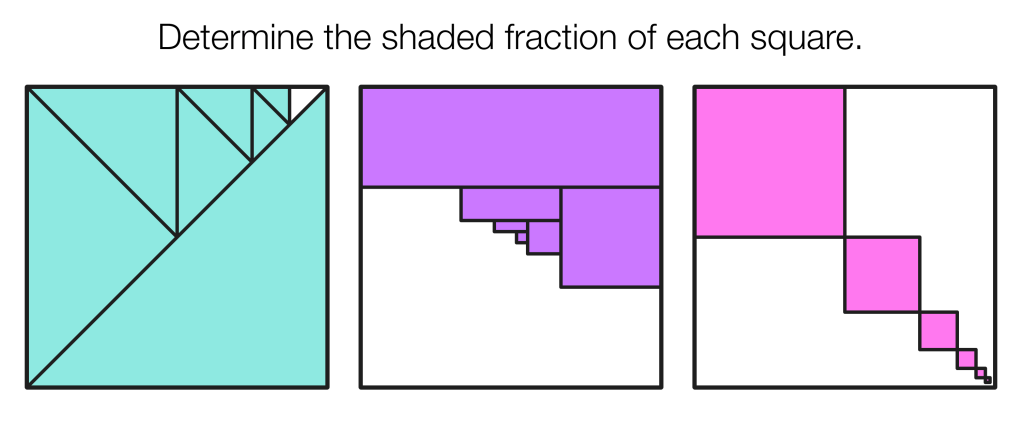
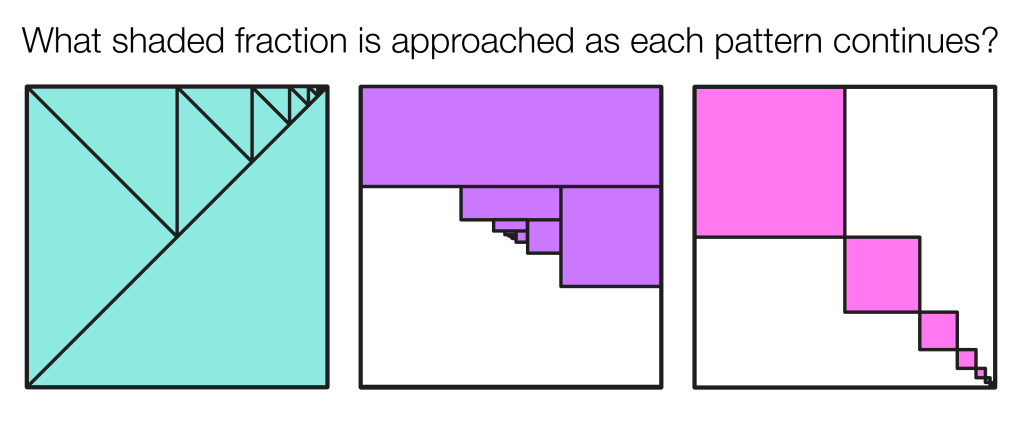








Pingback: Playful Math 179: Our Sweet Sixteen Carnival – Denise Gaskins' Let's Play Math